Motivation and Goal

In simple terms, the tree-breadth of a graph $G$ (written as $\mathrm{tb}(G)$) states how close $G$ is to a tree from a metric perspective. Strong tree-breadth (written as $\mathrm{stb}(G)$) follows the same idea, but it has some additional restrictions. It follows from their respective definitions that $\mathrm{tb}(G) \leq \mathrm{stb}(G)$ for each graph $G$. We currently do not know whether or not a limit on tree-breadth implies a limit on the strong tree-breadth of a graph. That is, we do not know if there isa constant $c$ such that $\mathrm{stb}(G) \leq c \cdot \mathrm{tb}(G)$ for each graph $G$. Recent results [2] suggest that such a boundary exits.

Although determining either parameter for a given graph is NP-complete, it is possible to estimate both parameters: A layering partition gives an upper bound of the tree-breadth of a graph [1]. Additionally, there is a polynomial algorithm that, if a given graph $G$ has strong tree-breath $\rho$, computes a tree-decomposition for $G$ withn (weak) tree-breadth at most $\rho$ [3].

For this project, Holly implemented the algorithms mentioned above. I then embedded her implementation into a server-client application that allows us to process both parameters on large graphs in parallel using multiple computers in a network. Our goal was to run them on various real-life net-works. The results might disprove some conjectures or give other indications for future theoretical research.

[1] F. Dragan, E. Köhler: An Approximation Algorithm for the Tree t-Spanner Problem on Unweighted Graphs via Generalized Chordal Graphs. Algorithmica 69 (4), 884-905, 2014.

[2] G. Ducoffe, A. Leitert: Equivalence Between Pathbreadth and Strong Pathbreadth. Discrete Applied Mathematics 262, 185-188, 2019.

[3] A. Leitert, F. Dragan: On Strong Tree-Breadth. COCOA 2016, Lecture Notes in Computer Science 10043, 62-76, 2016.

Programs

The project contains three programs:

• Server. The server coordinates the clients and combines their partial results into the overall result. It is written in C#.

  

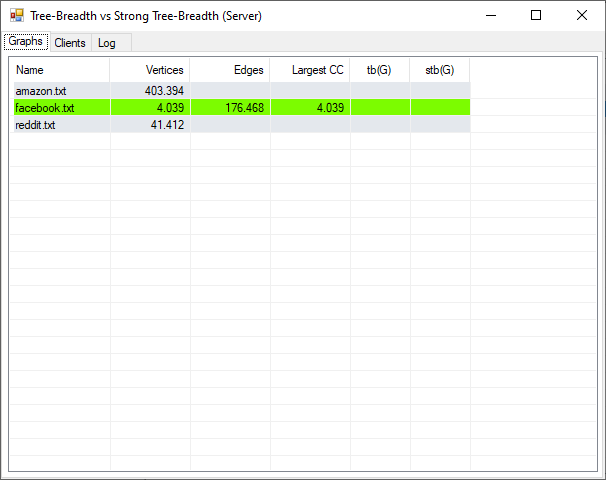
• Client. The client communicates with the server and computes what the server asks for. The computation of potential partners (to estimate strong tree-breadth) is forwarded to the according program (see below). Requests and results are communicated via standard-input and -output. The client is written in C#.

  

• Potential Partners (written by Holly). The program computes, for a given graph $G$ and vertex $v$, the potential partners of $v$ in $G$. Results are read by the client and then send to the server. The program is written in C++.